SandBox の履歴(No.2)

• 履歴一覧
• 差分 を表示
• 現在との差分 を表示
• ソース を表示
• SandBox へ行く。
  • 1 (2020-09-09 (水) 21:07:46)
  • 2 (2009-11-25 (水) 21:19:19)

SandBox: お砂場(練習ページ)です†

過去のものはどんどん消して構いません。 新しいものをどんどん書いて練習してください。 そう、ここは時々刻々と姿を変える砂場なのです。

mimeTeXの実験†

#mimeTeX{{ \begin{align}

 |\phi'|^2 &= (\phi'^\ast)(\phi') \\
           &= \left{e^{-i2\pi\left(\frac{L_1}{\lambda}-\nu t\right)} + e^{-i2\pi\left(\frac{L_2}{\lambda}-\nu t\right)} \right}\left{e^{i2\pi\left(\frac{L_1}{\lambda}-\nu t\right)} + e^{-i2\pi\left(\frac{L_2}{\lambda}-\nu t\right)} \right} \\
           &= 2 + e^{i2\pi\cdot\frac{L_1-L_2}{\lambda} } + e^{-i2\pi\cdot\frac{L_1-L_2}{\lambda} } \\
           &= 2 + 2\cos{2\pi\cdot\frac{L_1-L_2}{\lambda} } \\
 L_1 - L_2 &= \sqrt{L^2 + \left(y-\frac{d}{2}\right)} \\
           &= L\left[\left{1+\frac{1}{2}\left(\frac{y-\frac{d}{2} }{L}\right)^2\right} - \left{1+\frac{1}{2}\left(\frac{y+\frac{d}{2} }{L}\right)^2\right}\right] \\
           &= L\cdot\frac{-yd-2d}{2L^2} \\
           &= -\frac{yd}{L}

\end{align} }}

#mimeTeX{{

 f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-x_0)^2}{2\sigma^2} }

}}

#mimeTeX{{

 {\Bigint}^\infty_{-\infty} e^{-a^2x^2+bx}dx = \frac{\sqrt{\pi} }{a}e^{\frac{b^2}{4a^2} }

}}

＜P＞

最小化

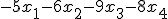
条件

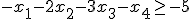
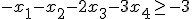
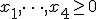
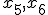1. ＜P＞をスラック変数（）を入れて等式標準系<P1>にせよ．

1. ＜P1＞の双対問題＜D1＞を書け．

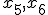1. （)を基底変数とする辞書を書き，基底解とその目的関数値を記せ．

1. 3.の辞書から単体法を行い，最適辞書を求めよ．また，そのときの最適解，最適値を記せ．

1. 双対問題＜D1＞の最適解と最適値を求めよ．

A4に書いて提出．期限は2009-12-09(水)

あれぇ，mimeTeXが機能しない．

#ref(): File not found: "suuri.dvi" at page "SandBox"

あれぇ、目的関数が間違ってるぞｗ

suuri.dviの目的関数に「4」が余計。texファイルを学校に置き忘れてきたので直せない（打ち直すのめんどいから直さない）けど。

sub, supの実験†

2^a₁